Notes on causal inference with No Overlap – Regression Discontinuity
Here is my notes on regression discontinuity from Prof. Ding’s textbook (2024) and Prof. Imai’s lecture notes.
Motivation
We often cannot run a randomized experiment and have to use/design observational studies to find a setting where credible causal inference is possible.
The key is the knowledge of treatment assignment mechanism.
Regression discontinuity design (RD Design):
RD Design is a simple and widely used quasi-experimental design. The term “quasi experimental” is to emphasize that these approaches are still framed using concepts from randomized experiments but require econometric innovations to compensate for the lack of random treatment assignment.
-
Sharp RD Design: treatment assignment is based on a deterministic rule (i.e. we have full knowledge of how treatment is assigned)
-
Fuzzy RD Design: encouragement to receive treatment is based on a deterministic rule
Setting
-
Binary treatment
-
Potential outcomes
-
There is a running variable
-
The unconfoundedness assumption holds automatically
-
The overlap assumption does not hold
Identification
-
RD can identify a local average causal effect at the cutoff point
-
Estimand:
-
Assumption 1 (continuity assumption).1.
2.
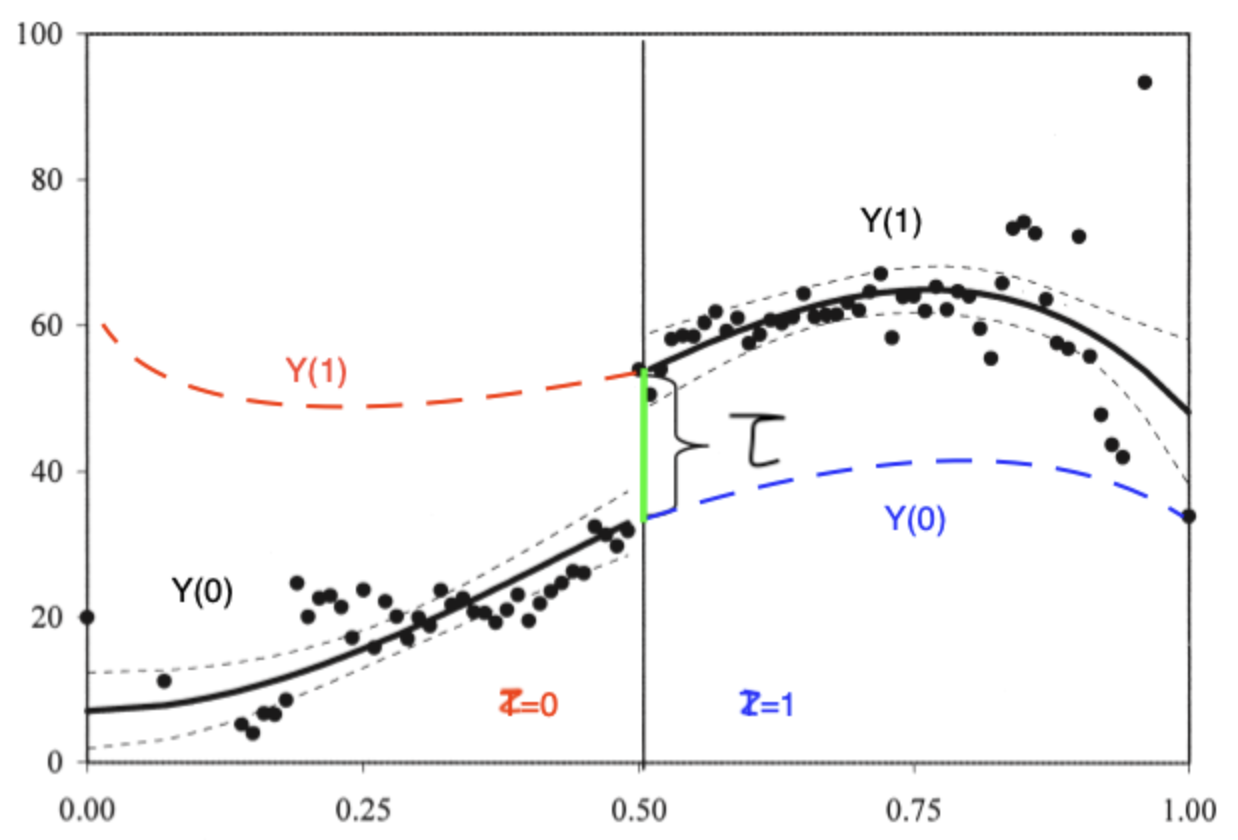
-
We have
-
Advantage: internal validity
-
Disadvantage: external validity
Key Theorem
Reference
Ding, P. (2024). A First Course in Causal Inference. CRC Press.