Notes on Callaway & Sant’Anna (2021) – Staggered Adoption DiD
0. Motivation
Staggered‐adoption policies break the canonical two-period / two-group DiD model. It has been shown that the traditional two-way fixed-effects (TWFE) regression can assign negative weights to treatment effects, thereby obscuring their dynamic and heterogeneous patterns.
Callaway & Sant’Anna (2021) propose a divide-and-conquer strategy:
-
Divide the messy staggered panel into many honest
-
Conquer by estimating each “little” DiD under familiar assumptions, then combine them with user-chosen weights to answer specific questions
The key takeaway:
-
Use
-
Many different aggregation schemes are possible: they deliver different parameters
-
Can allow for covariates via regressions adjustments, IPW, and DR.
1. Setup
-
Data structure: Panel of units
-
Let
-
Cohorts
-
Define
-
Define
-
Define
-
-
Potential outcomes
-
-
-
-
Cohort-time ATT
Assume
2. Key Assumptions
Given that we never observe
The no anticipation assumption has exactly the same content as in the
Note that, (1) is equivalent to the following: for
Similarly, (2) is equivalent to (2’), that is, changing
3. Identification: Long-Difference Estimands
Under no anticipation and one of the parallel-trends assumptions, each
- Using never-treated
- Using not-yet-treated
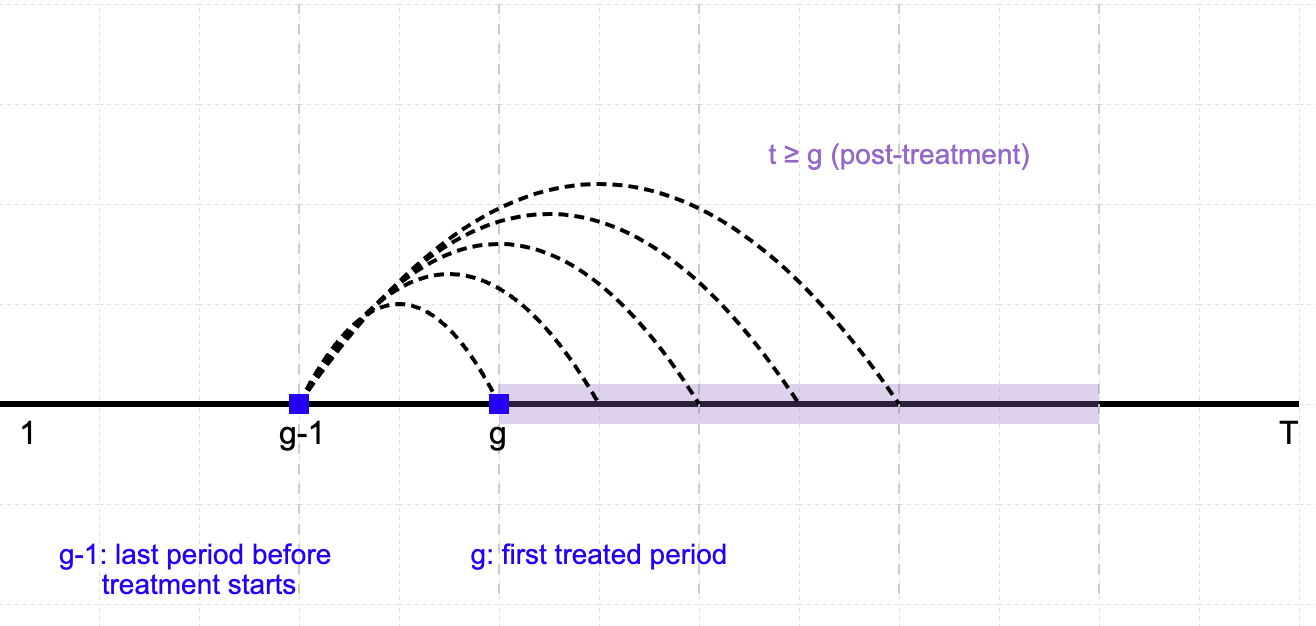
A: Longer Time Span! Check my plot above. The "long difference" refers to the fact that the comparison often spans from a pre-treatment period (i.e.
For each treated cohort, the method computes the difference in outcomes between the pre-treatment period and a specific post-treatment period, potentially far apart in time. This extended gap emphasizes the "long" aspect, as it captures the cumulative effect of the treatment over time.
Moreover, with covariates, one can form doubly-robust estimators that combine generalized propensity scores
For more details, check Theorem 1 in the paper.
4. Aggregation of
Any overall summary
Common choices:
- Cohort-heterogeneity: Average effect of participating in the treatment that units in group
-
Calendar time heterogeneity
-
Event-study / dynamic treatment effects
5. Limitation & Extension
Lee & Wooldridge (2023) argue that Callaway & Sant’Anna (2021) method is less efficient but more resilient to functional form of covariates. The followings are from their working paper:
… CS (2021) method uses only the period just prior to the intervention in defining the control group, thereby discarding potentially useful information in earlier time periods.
In fact, Wooldridge (2021) shows that, under the standard “error components” structure on the error, with a homoskedastic time-constant component and homoskedastic and serially uncorrelated idiosyncratic errors, the POLS estimator is both best linear unbiased (BLUE) and asymptotically efficient. These theoretical results imply that the CS (2021) estimators are inefficient under a standard set of assumptions. The simulations in Wooldridge (2021) bear this out, showing the CS approach can be very inefficient. Balanced against the loss in precision is that the CS approach can be less biased when parallel trends are violated.
To improve the efficiency, instead of using long differences, Lee and Wooldridge (2023) use all suitable control observations in transforming the outcome variable. Specifically, rather than using the single period just prior to the treatment,
The rolling method (Lee and Wooldridge, 2023) transforms panel data with staggered interventions by subtracting each unit’s average outcome across all pre-treatment periods from their outcome in the current period of interest. This transformation, combined with no anticipation and parallel trends assumptions, makes the treatment assignment unconfounded for the transformed outcome in each cohort/time cross-section. With unconfoundedness holding, we can then apply standard treatment effects estimators, including doubly robust methods and matching, utilizing all not-yet-treated units as the valid control group for that specific cross-section.
6. R code Example
The following R code example is provided by Professor Scott Cunningham.
library(readstata13)
library(ggplot2)
library(did) # Callaway & Sant'Anna
castle <- data.frame(read.dta13('https://github.com/scunning1975/mixtape/raw/master/castle.dta'))
castle$effyear[is.na(castle$effyear)] <- 0 # untreated units have effective year of 0
# Estimating the effect on log(homicide)
atts <- att_gt(yname = "l_homicide", # LHS variable
tname = "year", # time variable
idname = "sid", # id variable
gname = "effyear", # first treatment period variable
data = castle, # data
xformla = NULL, # no covariates
#xformla = ~ l_police, # with covariates
est_method = "dr", # "dr" is doubly robust. "ipw" is inverse probability weighting. "reg" is regression
control_group = "nevertreated", # set the comparison group which is either "nevertreated" or "notyettreated"
bstrap = TRUE, # if TRUE compute bootstrapped SE
biters = 1000, # number of bootstrap iterations
print_details = FALSE, # if TRUE, print detailed results
clustervars = "sid", # cluster level
panel = TRUE) # whether the data is panel or repeated cross-sectional
# Aggregate ATT
agg_effects <- aggte(atts, type = "group")
summary(agg_effects)
# Group-time ATTs
summary(atts)
# Plot group-time ATTs
ggdid(atts)
# Event-study
agg_effects_es <- aggte(atts, type = "dynamic")
summary(agg_effects_es)
# Plot event-study coefficients
ggdid(agg_effects_es)
Reference
Callaway, Brantly and Pedro H. C. Sant’Anna (2021), “Difference-in-Differences with multiple time periods,” Journal of Econometrics, Themed Issue: Treatment Effect 1, 225 (2), 200–230.
Lee, S. J., & Wooldridge, J. M. (2023). A Simple Transformation Approach to Difference-in-Differences Estimation for Panel Data (SSRN Scholarly Paper No. 4516518). Social Science Research Network. https://doi.org/10.2139/ssrn.4516518
Sant’Anna, Pedro H. C. and Jun Zhao (2020), “Doubly robust difference-in-differences estimators,” Journal of Econometrics, 219 (1), 101–22.
How does doubly robust DiD estimator works? Check this: Lecture 5: How Covariates can make your DiD More Plausible
did R package 📦