Triply Robust Panel Estimators 🛡: When You Don't Know Which Assumptions Hold
TL;DR
Athey, Imbens, Qu, and Viviano introduce the Triply RObust Panel (TROP) estimator, which combines unit weights, time weights, and a flexible low-rank factor model to estimate causal effects in panel data. The estimator achieves triple robustness: it remains unbiased if any one of three components succeeds (unit balance, time balance, or correct outcome modeling). Across 21 empirically calibrated simulation designs, TROP outperforms standard methods like DID, synthetic control, matrix completion, and synthetic difference-in-differences in 20 out of 21 cases, often by substantial margins. The method is particularly valuable when interactive fixed effects violate parallel trends assumptions and when researchers face uncertainty about which modeling assumptions hold.
What is this paper about?
This paper addresses a fundamental challenge in panel data analysis: choosing among competing estimators when the validity of their underlying assumptions is uncertain. Traditional difference-in-differences (DID) methods assume parallel trends, synthetic control (SC) emphasizes pre-treatment outcome alignment, and matrix completion (MC) relies on low-rank factor structures, but researchers rarely know which assumptions hold in practice. A second problem is that existing methods often treat observations uniformly across time and units, ignoring that recent periods may be more informative for predicting counterfactuals than distant ones, and that some control units may be more comparable to treated units than others. Third, most SC-based methods are designed for a single treated unit and do not naturally extend to complex assignment patterns with multiple treated units and staggered adoption. The authors propose a unified framework that addresses all three issues simultaneously while providing formal robustness guarantees.
What do the authors do?
The authors develop the TROP estimator, which minimizes a weighted regression objective that incorporates:
-
unit-specific weights (to upweight control units similar to treated units)
-
time-specific weights (to upweight recent periods)
-
a nuclear-norm-penalized low-rank factor model (to capture interactive fixed effects)
They propose an exponential decay structure for time weights and distance-based weights for units, with all tuning parameters selected via leave-one-out cross-validation.
To evaluate performance, they conduct extensive semi-synthetic simulations calibrated to seven real datasets (CPS wage data, Penn World Table GDP, Germany reunification, Basque country, California smoking, and Mariel boatlift), generating outcomes from rank-4 factor models with realistic autocorrelation and treatment assignments based on estimated propensity scores from actual policies. They systematically vary features of the data-generating process (removing autocorrelation, interactive effects, or fixed effects) and components of the estimator (shutting down unit weights, time weights, or the regression adjustment) to understand what drives performance differences. They provide formal theory showing that TROP’s bias equals the product of (1) unit imbalance, (2) time imbalance, and (3) regression model misspecification, establishing triple robustness.

Why is this important?
The paper makes three critical contributions to applied panel data analysis. First, it demonstrates that interactive fixed effects—where unit-specific trends vary over time—are empirically pervasive and cause substantial bias in standard DID estimators, with violations present in over 58% of units across their applications and adding even a single interactive factor reducing RMSE by 10-60%. Second, it shows that no single existing method dominates: DID can have RMSE 900% higher than the best competitor in some settings, SC can be 580% worse, and even modern methods like SDID can be 90% worse, highlighting the risk of mechanically applying any one approach. Third, TROP provides a principled solution by learning from the data which components (unit balance, time balance, or factor modeling) matter most for each application, offering insurance against model misspecification without requiring researchers to know ex ante which assumptions hold. The triple robustness property means that getting any one of three components approximately right suffices for consistency, substantially weakening the conditions needed for valid causal inference.
Who should care?
Applied researchers using panel data methods to evaluate policies, interventions, or natural experiments should care deeply about this paper, especially those working with observational data where parallel trends may fail due to heterogeneous trends across units. Economists studying labor markets, public finance, development, or industrial organization who face settings with staggered treatment adoption or multiple treated units will benefit from the method’s flexibility. Methodologists interested in robust causal inference, doubly robust estimation, or combining machine learning with causal identification will find the theoretical framework valuable. Policy analysts and data scientists in government agencies producing impact evaluations need methods that perform well under uncertainty about modeling assumptions. Anyone who has abandoned a difference-in-differences project because pre-trends failed should reconsider whether allowing for interactive fixed effects and flexible weighting could recover valid identification.
Do we have code?
The paper does not provide replication code, R or Python packages, or links to implementation files. The method requires implementing nuclear-norm-penalized regression combined with weighted least squares and a cross-validation procedure to select three tuning parameters (λ_unit, λ_time, λ_nn), which is computationally involved but feasible for researchers comfortable with optimization. The algorithms are described in detail (Algorithms 1-3 in the paper), and the exponential decay weighting scheme and distance metrics are explicitly specified in equations (3) and surrounding text. Researchers would need to build their own implementation or wait for the authors to release software, though the paper’s clarity makes this more tractable than usual.
In summary, this paper introduces a methodologically sophisticated yet practically motivated estimator that combines the strengths of synthetic control (unit weighting), modern DID approaches (time weighting), and matrix completion (low-rank modeling) while avoiding the brittleness of relying on any single component. The extensive simulations demonstrate that TROP consistently outperforms existing methods across diverse empirically relevant settings, with the advantage most pronounced when interactive fixed effects are present—a common feature of real data that violates standard parallel trends assumptions. The triple robustness property provides formal theoretical insurance: if researchers get unit balance approximately right, or time balance approximately right, or the factor model approximately right, the estimator remains consistent. For applied work, this represents a major advance in practical robustness, moving beyond the “which method should I use?” question to “let the data tell us which features matter most." The lack of available code is the main practical limitation, but the clear exposition of algorithms makes implementation feasible for quantitatively oriented researchers.
Points I enjoyed
TROP vs. SDID
Let’s compare the TROP vs. SDID:
-
Triple Robustness (TROP): TROP achieves triple robustness, meaning its asymptotic bias vanishes if either the unit weights, or the time weights, or the flexible low-rank regression adjustment successfully remove the underlying biases. The bias of TROP depends on the product of unit imbalance, time imbalance, and the bias arising from a potentially misspecified regression adjustment.
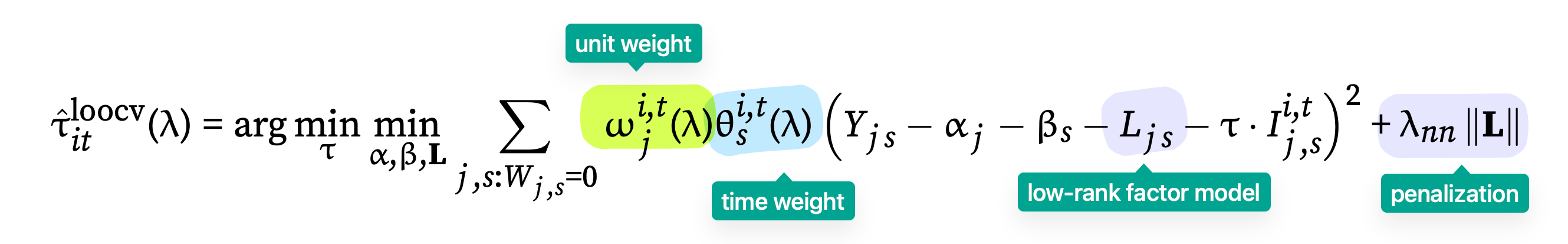
Figure 2: Key difference between TROP and SDID – adding the low-rank factor component in the outcome model -
Double Robustness (SDID): SDID (Arkhangelsky et al. 2021) achieves only double robustness, where bias vanishes if either unit imbalance or time imbalance is negligible. It lacks the third robust channel provided by the flexible regression adjustment.
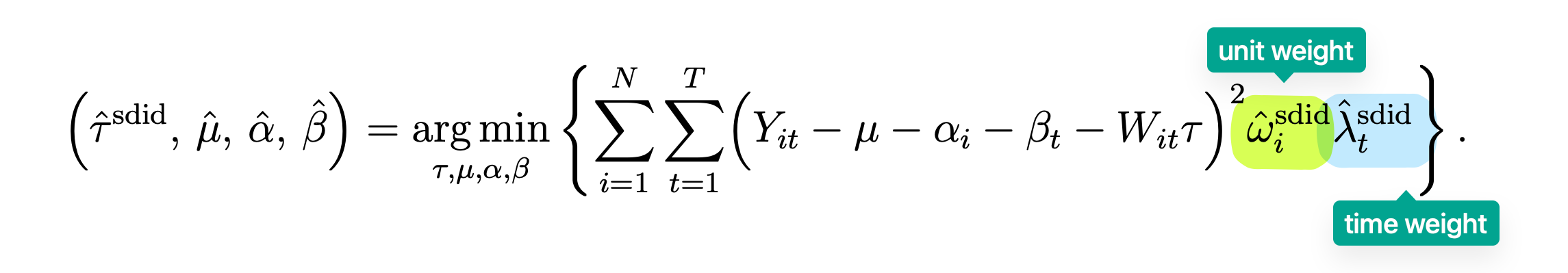
Figure 3: In SDID, there is no low-rank component
How to come up with this TROP estimator? My Thought
Recall that:
-
Matrix completion methods (Athey et al. 2021) focus solely on modeling the outcomes as a function of the latent factors. These methods aim to accurately model the control outcome process using a low-rank factor structure that generalizes the two-way fixed effects (TWFE) model
-
SDID is a “local” TWFE estimator, which essentially corresponds to modeling the assignment mechanism, via local weighting (i.e. unit and time weights)
The estimated average counterfactual from the TROP estimator has the following form:

It contains both unit/time weights (the key idea in SDID) and outcome model (low-rank factor model) in matrix completion methods. The TROP estimator,
This form also reminds me the idea in AIPW estimator or the generic debiased framework (Chernozhukov, Newey, and Singh 2022) – leveraging the Riesz representer to correct for bias.

Chek more details from my previous post: “Intuition for Doubly Robust Estimator”.
Reference
Athey, Susan, Guido Imbens, Zhaonan Qu, and Davide Viviano (2025), “Triply robust panel estimators.” https://doi.org/10.48550/arXiv.2508.21536
Athey, Susan, Mohsen Bayati, Nikolay Doudchenko, Guido Imbens, and Khashayar Khosravi (2021), “Matrix Completion Methods for Causal Panel Data Models,” Journal of the American Statistical Association, 116 (536), 1716–30.
Arkhangelsky, Dmitry, Susan Athey, David A. Hirshberg, Guido W. Imbens, and Stefan Wager (2021), “Synthetic Difference-in-Differences,” American Economic Review, 111 (12), 4088–4118.
Chernozhukov, Victor, Whitney K. Newey, and Rahul Singh (2022), “Automatic Debiased Machine Learning of Causal and Structural Effects,” Econometrica, 90 (3), 967–1027.
