When Good Controls Aren't Good Enough: The Augmented Synthetic Control Method
Ben-Michael, Eli, Avi Feller, and Jesse Rothstein (2021), “The Augmented Synthetic Control Method,” Journal of the American Statistical Association, 116 (536), 1789–1803.
Key insight: Synthetic control method (SCM) can be regarded as a form of inverse propensity score weighting. The authors apply insights from AIPW and bias correction for matching. SCM is a special case of balancing weights estimation.
TL;DR
Ben-Michael, Feller, and Rothstein extend the synthetic control method (SCM) to settings where perfect pretreatment fit is infeasible. Their Augmented SCM (ASCM) uses an outcome model to estimate and correct bias from imperfect pretreatment balance, then de-biases the original SCM estimate. Ridge ASCM—their main proposal—directly controls pretreatment fit while minimizing extrapolation outside the convex hull of control units. Under both autoregressive and linear factor models, they show how regularization avoids overfitting to noise while improving finite-sample estimation error bounds.
What is this paper about?
The synthetic control method constructs a weighted average of control units (a “synthetic control”) that closely matches a treated unit’s pretreatment outcomes to estimate causal effects in panel data settings. A critical feature of the original SCM proposal is that it should only be used when pretreatment fit is excellent—when the synthetic control’s outcomes track the treated unit’s outcomes nearly perfectly before treatment. When such fit is impossible to achieve with nonnegative weights that sum to one (the “simplex constraint”), Abadie, Diamond, and Hainmueller recommended against using SCM at all. This leaves researchers in a difficult position: they can either abandon SCM and fall back on linear regression (which allows better fit but extrapolates outside the data support using negative weights), or they can use SCM despite poor pretreatment fit (risking substantial bias). This paper addresses that gap by proposing a method that navigates between these two extremes.
What do the authors do?
The authors develop Augmented SCM, which begins with the original SCM estimate, uses an outcome model to estimate the bias due to imperfect pretreatment fit, and then subtracts this estimated bias from the SCM estimate. Their primary proposal, Ridge ASCM, augments SCM with a ridge-regularized linear outcome model. They prove that Ridge ASCM weights can be expressed as the solution to a modified synthetic controls problem that penalizes deviation from the original SCM weights, allowing negative weights only when necessary to improve fit. The ridge penalty parameter directly controls the trade-off between bias reduction (through better pretreatment fit) and variance increase (through extrapolation). They derive finite-sample error bounds under both an autoregressive data-generating process and a linear factor model, showing how the regularization parameter negotiates bias-variance trade-offs and prevents overfitting to noise. They also extend the framework to incorporate auxiliary covariates and propose a cross-validation procedure for hyperparameter selection. Finally, they demonstrate the method’s performance through extensive calibrated simulations and apply it to estimate the effect of Kansas’s 2012 tax cuts on economic growth.
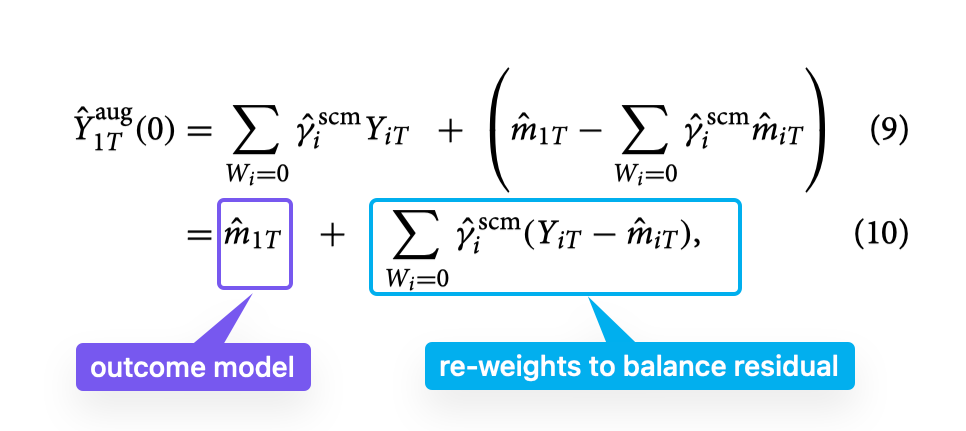
Why is this important?
The original SCM is powerful but deliberately limited: it works beautifully when excellent pretreatment fit is achievable, but the method’s creators explicitly warned against using it otherwise. This restriction excludes many practical applications where the treated unit lies outside the convex hull of control units—a common problem when the number of pretreatment periods is modest relative to the heterogeneity among units. Augmented SCM makes SCM-style approaches viable in these previously excluded settings without sacrificing the method’s core appeal: interpretability through sparse, mostly nonnegative weights. Unlike ridge regression alone, which can produce arbitrary negative weights even when unnecessary, Ridge ASCM only extrapolates when the treated unit cannot be represented as a convex combination of controls. The regularization parameter provides researchers with explicit, transparent control over how much extrapolation they’re willing to accept in exchange for bias reduction. This matters because extrapolation bias and covariate imbalance are often the dominant sources of error in comparative case studies, and Ridge ASCM provides a principled way to navigate that trade-off.
Who should care?
Applied researchers using comparative case studies with panel data—particularly in policy evaluation settings where a single treated unit (a state, city, or country) receives treatment and researchers need to construct a credible counterfactual. This includes economists studying state-level policy changes, political scientists examining the effects of institutional reforms, public health researchers evaluating localized interventions, and anyone working with “small N, large T” observational panel data. Methodologists working on causal inference in panel data settings and those interested in balancing methods, doubly-robust estimation, and synthetic controls will find the theoretical contributions valuable. The method is especially relevant when the treated unit’s characteristics place it on the periphery or outside the support of the control units, making perfect pretreatment balance with nonnegative weights impossible.
Do we have code?
Yes. The authors implement the proposed methodology in the augsynth R package, available at https://github.com/ebenmichael/augsynth. The package includes functions for Ridge ASCM, other augmentation approaches, hyperparameter selection via cross-validation, and conformal inference for uncertainty quantification.
In summary, this paper solves a significant practical limitation of synthetic control methods by allowing their use in settings where perfect pretreatment fit is infeasible. Ridge ASCM augments the original SCM estimate with a bias correction from a regularized outcome model, yielding weights that can be interpreted as a penalized synthetic control problem. The method explicitly controls extrapolation through the ridge penalty while improving pretreatment fit, and the authors show both theoretically and empirically that this approach reduces bias and mean squared error relative to SCM alone across a range of data-generating processes. By providing a middle ground between the restrictive conditions of traditional SCM and the unconstrained extrapolation of regression, Augmented SCM expands the toolkit for credible causal inference in comparative case studies.
Reference
Ben-Michael, Eli, Avi Feller, and Jesse Rothstein (2021), “The Augmented Synthetic Control Method,” Journal of the American Statistical Association, 116 (536), 1789–1803.
Arkhangelsky, Dmitry, Susan Athey, David A. Hirshberg, Guido W. Imbens, and Stefan Wager (2021), “Synthetic Difference-in-Differences,” American Economic Review, 111 (12), 4088–4118.