Notes on DML for DiD: A Unified Approach

Introduction

This blog post explores how Double Machine Learning (DML) extends to conditional Difference-in-Differences (DiD), focusing on doubly robust estimators. The key insight is that conditional DiD can be understood through the lens of cross-sectional ATT estimation.

Foundation: Cross-Sectional ATT Estimation

To build intuition, we start with the familiar cross-sectional setting. Standard identification requires three assumptions: SUTVA, unconfoundedness, and overlap.

Step 1: Propensity Score Approach for ATT

• Unlike ATE, ATT estimation requires only “one-sided” unconfoundedness and overlap conditions.

  Assumption 1 (Identification Assumptions).

  $$Z\perp \perp Y(0)\mid X\text{ and }e(X)<1$$

• Estimate ATT using IPW

  Theorem 1 (Ding (2024), Section 13.2).

  

• More general, Li et al. (2018a) gave a unified discussion of the causal estimands in observational studies.

  Theorem 2 (Ding (2024), Section 13.4).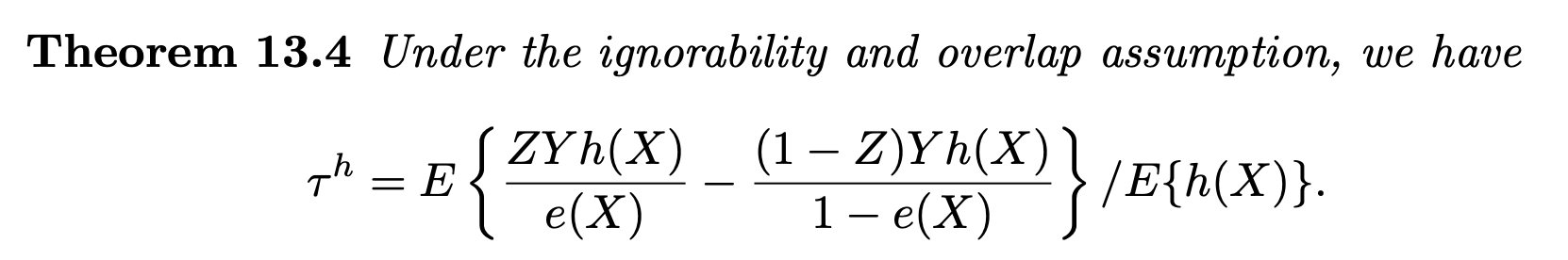

  
  Summary Table of common estimands:

  • This table provides us a good way to understand and remember IPW estimator for ATT

  • How to remember ${\tau }^h$? Apply IPW on “pseudo outcome” $Yh(X)$ then divide by $E(h(X))$

  • When the parameter of interest is ATT, then $$E(h(X))=E(e(X))=E(E(Z\mid X))=E(Z)=\mathbb{P}(Z=1)=e$$

  • Use it to better understand IPW for ATT

Step 2: Doubly Robust ATT Estimator

• Combines outcome regression and IPW methods

• For DR estimator of ATT, check my previous post

• More generally, we have

  Theorem 3 (DR for general estimand, see Ding (2024), page 191).

  

Extension to Conditional DiD

Identification Assumptions

Conditional DiD relies on two core assumptions: conditional parallel trends and no anticipation, plus an overlap condition.

Assumption 2 (CausalML Book, page 457).

• How to understand the overlap condition (16.3.3)? It essentially imposes that there are control observations available for every value of $X$.

The Key Insight: Transformation to Cross-Sectional Problem

By taking the difference,

$$\mathrm{\Delta }Y=Y_{\text{after}}-Y_{\text{before}}$$

we transform panel data into a cross-sectional problem. This allows us to apply the same doubly robust framework used for cross-sectional ATT.

The Unified Result

The Neyman orthogonal score for conditional DiD is identical to the cross-sectional ATT score, where the outcome variable is simply the difference $\mathrm{\Delta }Y$.

• Neyman orthogonal score for ATT in conditional DiD

  Proposition 1 (see CausalML Book).

  

• Neyman orthogonal score for ATT in cross-sectional setting

  Proposition 2 (see CausalML Book).

  
  

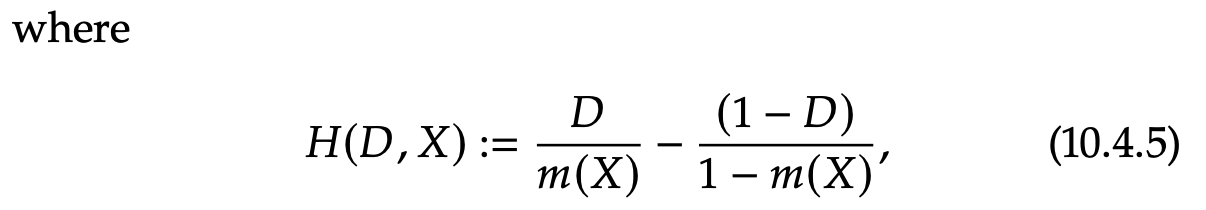
• Comparing to the score for the ATT in cross-sectional setting, we see that DiD score is identical to that for learning the ATT under unconfoundedness where the outcome variable is simply defined as $\mathrm{\Delta }Y$

References

Chernozhukov, Victor, Christian Hansen, Nathan Kallus, Martin Spindler, and Vasilis Syrgkanis (2024), “Applied causal inference powered by ML and AI.”

Ding, P. (2024). A First Course in Causal Inference. CRC Press.

Callaway, Brantly and Pedro H. C. Sant’Anna (2021), “Difference-in-Differences with multiple time periods,” Journal of Econometrics, Themed Issue: Treatment Effect 1, 225 (2), 200–230.

Chernozhukov, Victor, Whitney K Newey, and Rahul Singh (2022), “Debiased machine learning of global and local parameters using regularized Riesz representers,” The Econometrics Journal, 25 (3), 576–601.

Chernozhukov, Victor, Whitney K. Newey, Victor Quintas-Martinez, and Vasilis Syrgkanis (2024), “Automatic debiased machine learning via riesz regression.”