Note for Beta Distribution
This post is out of date, please check the new post named “Beta Distribution — Intuition, Derivation, and Examples”.
1 Why Beta Distribution?
1.1 Model probabilites
The short story is that the Beta distribution can be understood as representing a distribution of probabilities, that is, it represents all the possible values of a probability when we don’t know what that probability is.
1.2 Generalization of uniform
Give me a continuous and bounded random variable, em, except the Uniform distribution. That is another way to look at beta distribution, continuous and bounded between 0, 1; also the density is not flat.
What is
2 Construction
2.1 Bank and Post Office Story
Let
Let
Assume
Then, what is the distribution of the proportion
Define
Clearly,
Define
What is the distribution of
We need to derive
Then we find the marginal,
Since
so the normalization constant should be
2.1.1 Summary
The connection between Gamma and Beta distribution helps us to find the normalization constant in Beta. In summary,
If
2.2 plots
library(zetaEDA)
library(ggfortify)
enable_zeta_ggplot_theme()Let’s check Beta density for some different parameters value.
How about
ggdistribution(func = dbeta, x = seq(0, 1, .01), shape1 = 1, shape2 = 1) +
labs(title = "Beta Density with a = 1, b = 1")
How about
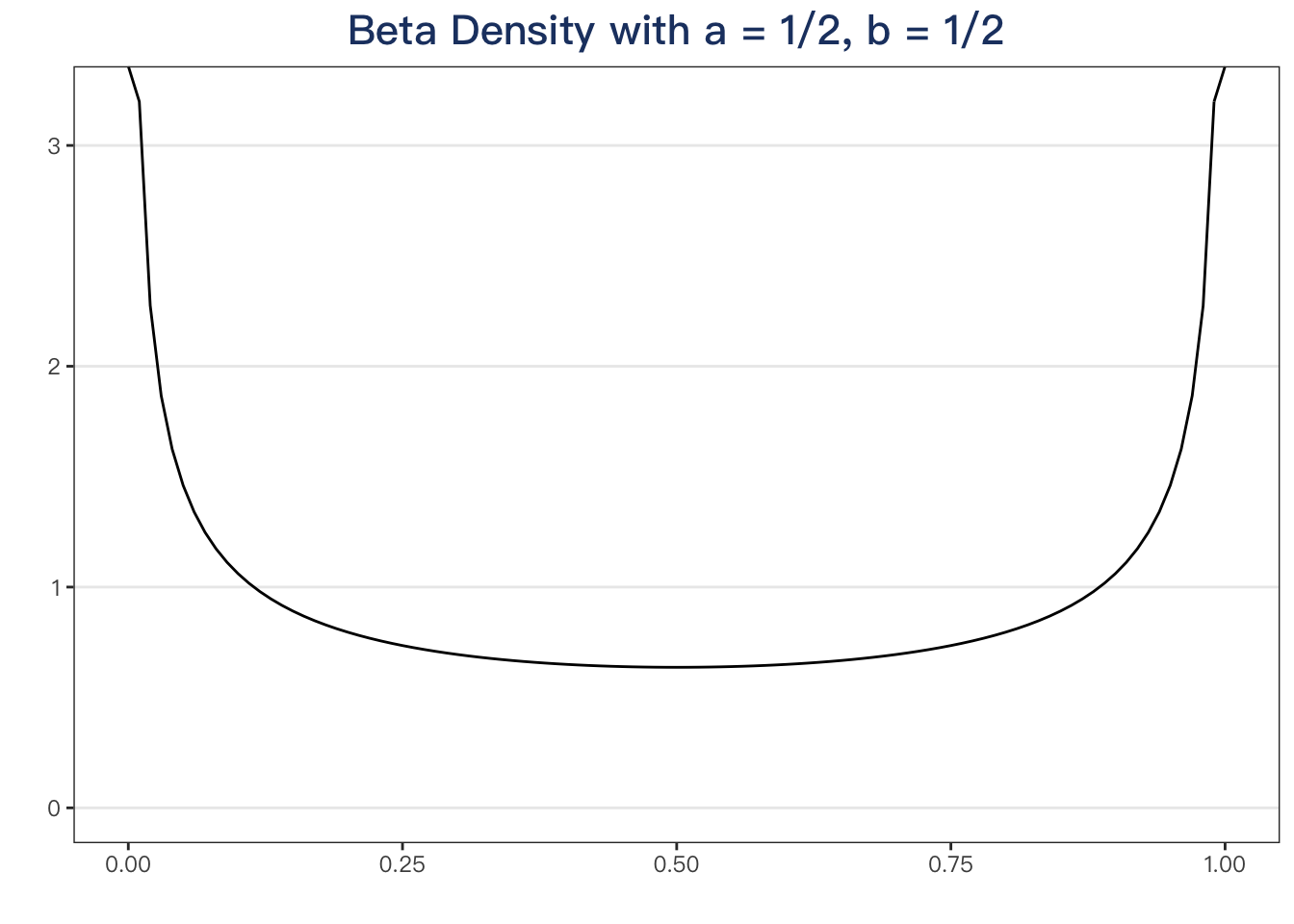
How about
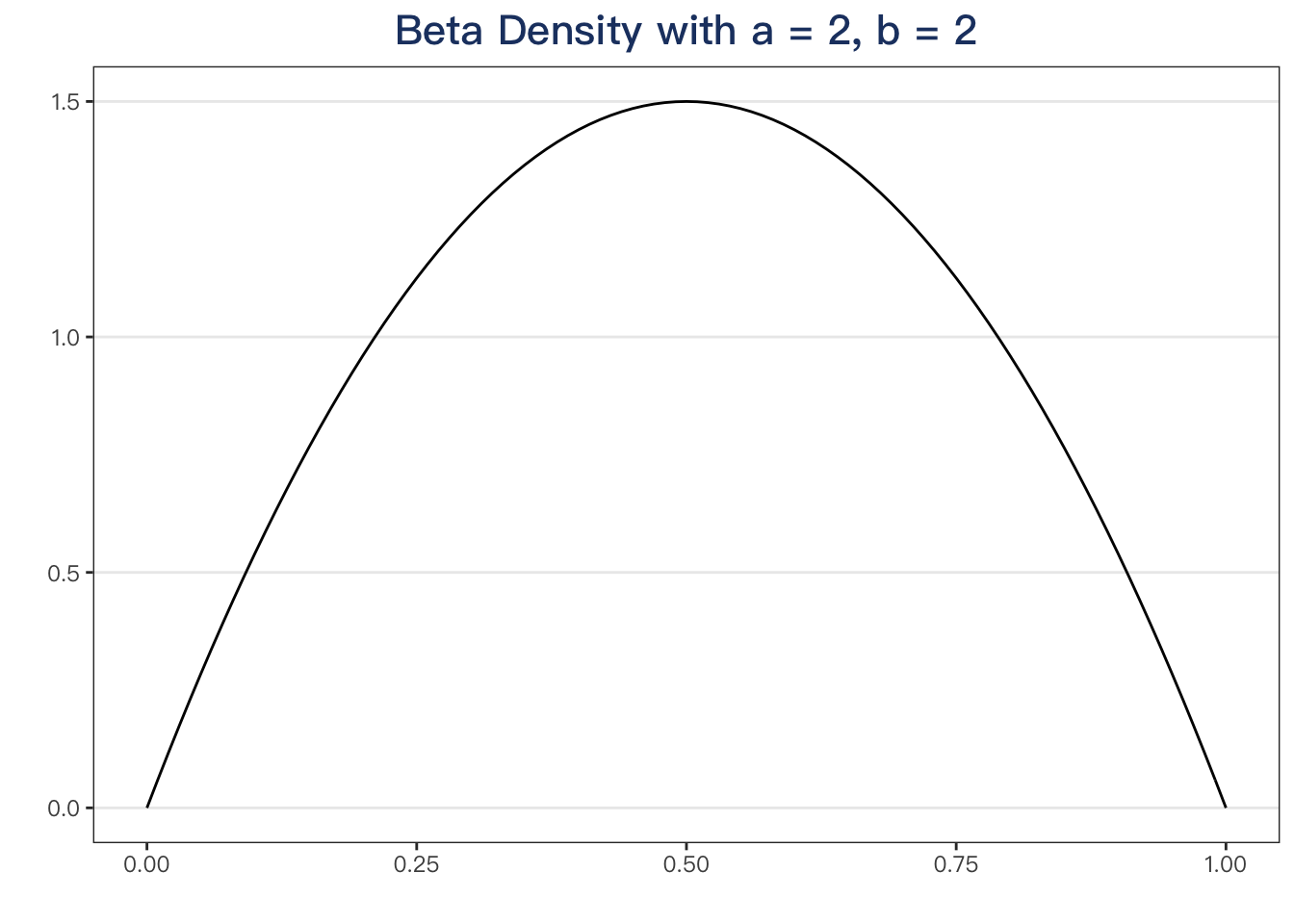
How about
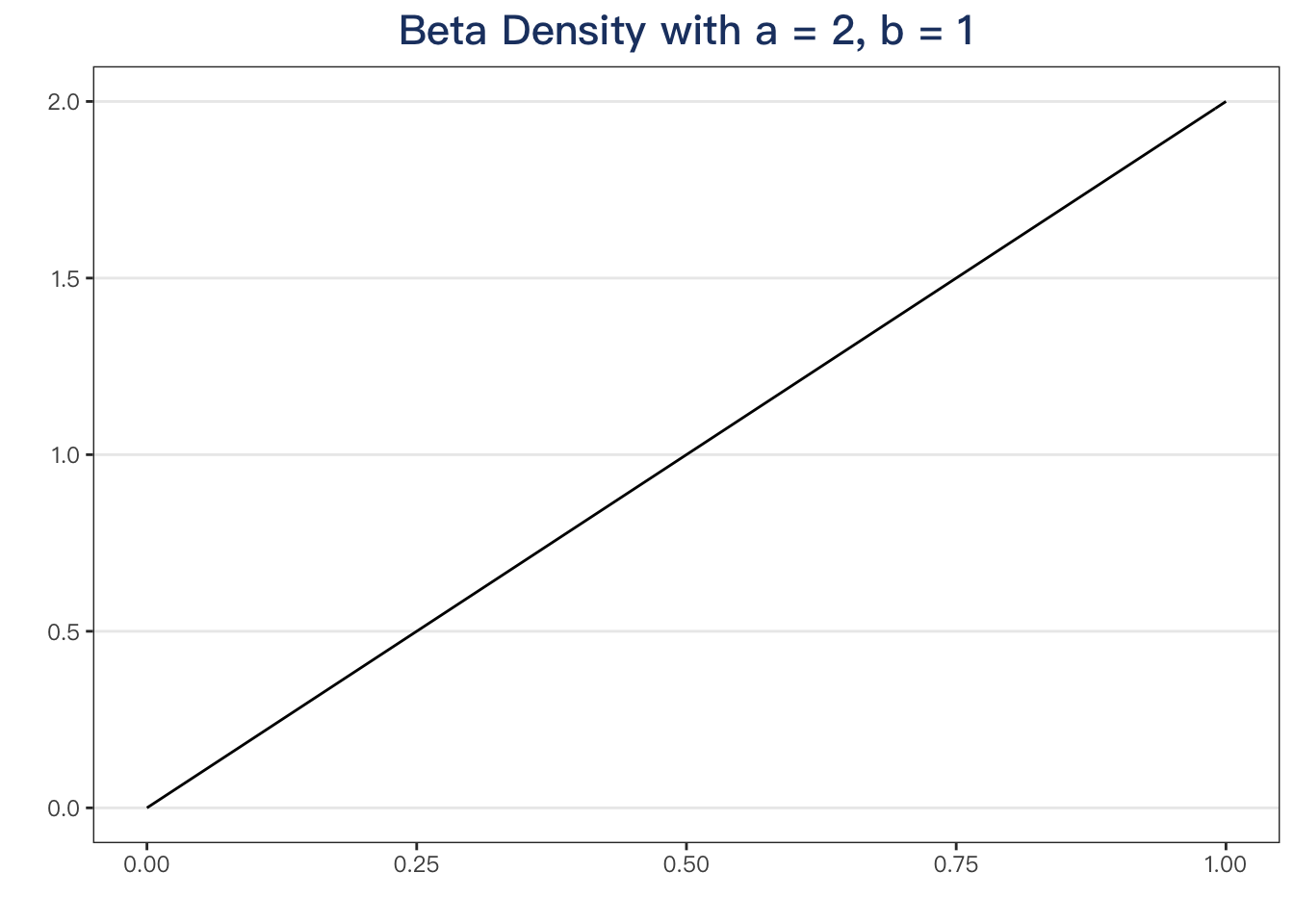
One more,
p <- ggdistribution(func = dbeta, x = seq(0, 1, .01), shape1 = 1.5, shape2 = 5, colour = "tomato", linetype = "dashed")
ggdistribution(func = dbeta, x = seq(0, 1, .01), shape1 = 5, shape2 = 1.5, colour = "blue", p = p) +
labs(title = "Red: a = 1.5, b = 5\n Blue: a = 5, b = 1.5")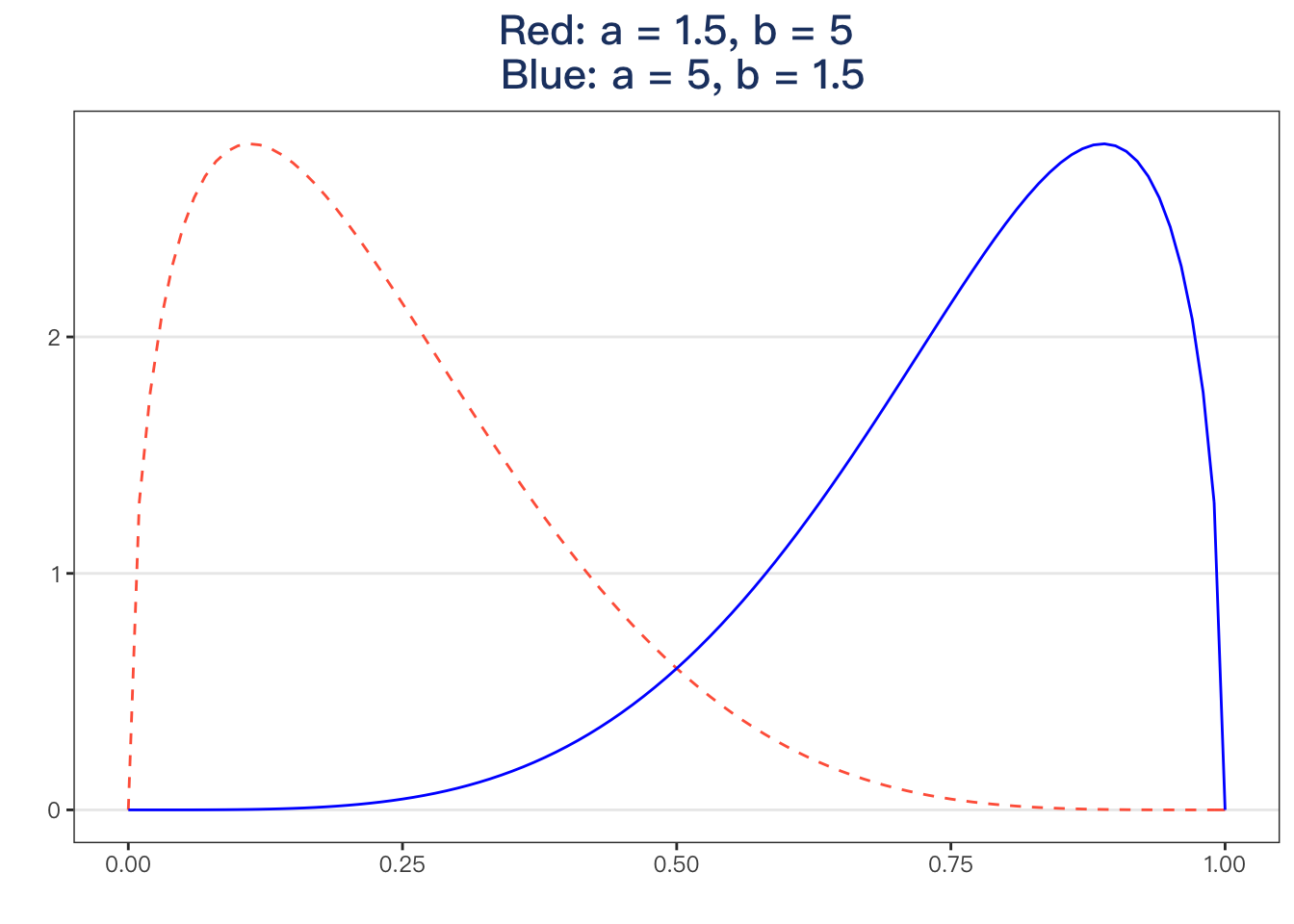
For more checking, click this link and try some parameters to check the density curve.
Have fun!