1.1 Some notation

For an customer,

Define:

$$x=\text{the number of purchase,}$$

$$t_i=\text{the time of ith purchase},\text{ where }1\le t_i\le t_x,$$

$$t_x=\text{the time of last purchase in the history,}$$

$$T=\text{total time being observed}$$

Next, we’ll show that it is sufficient to use individual’s $(x,t_x,T)$ to describe his/her purchase behavior in Pareto/NBD model.

1.2 Conditional on $\lambda$ and $\mu$

Assume a customer’s $x$ transactions occurred during the period $(0,T]$; we denote these times by $t_1,t_2,t_3,\cdots ,t_x$.

There are two possible ways this pattern of transactions could arise:

1. The customer is still alive at the end of the observation period (i.e., $\tau >T$ ), the individual-level likelihood function is simply the product of the (inter-transaction-time) exponential pdf and the associated survivor function:

2. The customer became inactive at some time $\tau$ in the interval $(t_x,T]$ (i.e. $\tau \in (t_x,T]$), in which case the individual-level likelihood function is

Note that in both cases, information on when each of the x transactions occurred is not required.

We can replace $t_1,...t_x$ , $T$ with $(x,t_x,T)$ where, by definition, $t_x=0$ when $x=0$. In other words, $t_x$, $x$ and $T$ are sufficient summaries of a customer’s transaction history. Using direct marketing terminology, $t_x$ is recency and $x$ is frequency.

由以上两个事实可知，无需知晓客户每次的购买时间，第一次消费时间、最后一次消费时间、消费频次 作为充分统计量，已经足够我们导出似然函数了！

Removing the conditioning on $\tau$ gives us the following expression for the individual-level likelihood function:

1.3 Removing the Conditioning on $\lambda$ and $\mu$

We remove the conditioning on $\lambda$ and $\mu$ by taking the expectation of $L(\lambda ,\mu |x,t_x,T)$ over the distributions of $\lambda$ and $\mu$ :

$$L(r,\alpha ,s,\beta \mid x,t_x,T)={\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}L(\lambda ,\mu \mid x,t_x,T)g(\lambda \mid r,\alpha )g(\mu \mid s,\beta )d\lambda d\mu$$

The computation is tedious, check the paper “A Note on Deriving the Pareto/NBD Model and Related Expressions” to know the details.

1.4 MLE for $r,\alpha ,s,\beta$

Since we have derived the likelihood function $L(r,\alpha ,s,\beta \mid x,t_x,T)$, the 4 Pareto/NBD model parameters $(r,\alpha ,s,\beta )$ can be estimated via the method of MLE. Specifically, suppose we have a sample of $N$ customers, where customer $i$ had $x_i$ transactions in the period $(0,T_i]$, with the last transaction occurring at $t_{x_i}$ . The sample log-likelihood function is given by

$$LL(r,\alpha ,s,\beta )=\sum _{i=1}^N\ln \left[L(r,\alpha ,s,\beta \mid x_i,t_{x_i},T_i)\right].$$

This can be maximized using standard numerical optimization routines. Therefore, we will obtain 4 maximum likelihood estimators $(\hat{r},\hat{\alpha },\hat{s},\hat{\beta })$

2.1 Mean of the Pareto/NBD Model

Given that the number of transactions follows a Poisson process while the customer is alive,

1. if $\tau >t$, the expected number of transactions is simply $\lambda t$.
2. if $\tau \le t$, the expected number of transactions in the interval (0, τ] is $\lambda \tau$.

Removing the conditioning on the time at which the customer becomes inactive, it follows that the expected number of transactions in the time interval $(0,t]$, conditional on $\lambda$ and $\mu$, is

$$\begin{array}{rl}E[X(t)\mid \lambda ,\mu ]& =\lambda tP(\tau >t\mid \mu )+{\int }_0^t\lambda \tau f(\tau \mid \mu )d\tau \\ & =\lambda t{e}^{-\mu t}+\lambda {\int }_0^t\mu \tau e^{-\mu \tau }d\tau \\ & =\lambda t{e}^{-\mu t}+\frac{\lambda }{\mu }{\int }_0^t{\mu }^2\tau e^{-\mu \tau }d\tau ,\text{where integrand is an Erlang-2}\\ & =\lambda t{e}^{-\mu t}+\frac{\lambda }{\mu }\{1-e^{-\mu t}-\mu t{e}^{-\mu t}\}\\ & =\frac{\lambda }{\mu }-\frac{\lambda }{\mu }{e}^{-\mu t}\end{array}$$

Now removing the Conditioning on $\lambda$ and $\mu$,

2.2 Derivation of PAlive

The probability that a customer with purchase history $(x,t_x,T)$ is “alive” at time $T$ is $P(\tau >T)$.

As the $\lambda$ and $\mu$ are unobserved, we compute $P(alive|x,t_x,T)$ for a randomly-chosen individual by taking the expectation of the above result over the distribution of $\lambda$ and $\mu$ , updated to take account of the information $(x,t_x,T)$:

By Bayes’ theorem, the joint posterior distribution of $\lambda$ and $\mu$ is

$$g(\lambda ,\mu \mid r,\alpha ,s,\beta ,x,t_x,T)=\frac{L(\lambda ,\mu \mid x,t_x,T)g(\lambda \mid r,\alpha )g(\mu \mid s,\beta )}{L(r,\alpha ,s,\beta \mid x,t_x,T)}$$

Thus,

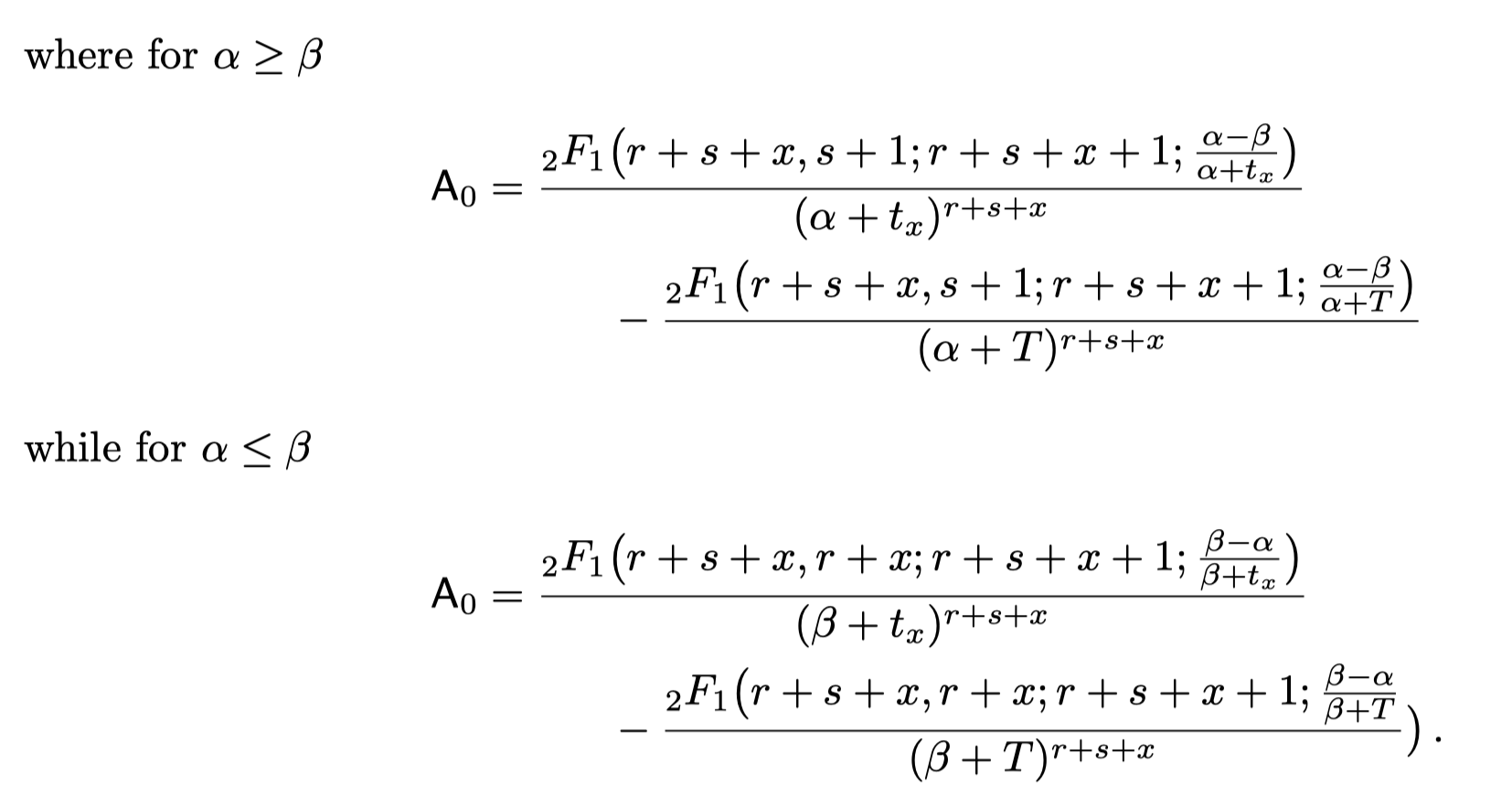
For details check the reference paper. Note that, the above result is the formula to calculate PAlive used in BTYD 📦 implemented in R.

2.3 Conditional Expectation of Transactions

Let random variable $Y(t)=\text{num of purchase made in }(T,T+t]$. We are interested in computing $E(Y(t)|x,t_x,T)$, the expected number of purchase in the period $(T,T+t]$ for a customer with purchase history $(x,t_x,T)$.

If the customer is active at $T$,

$$\begin{array}{ll}& E[Y(t)\mid \lambda ,\mu ,\text{ alive at }T]\\ & =\lambda tP(\tau >T+t\mid \mu ,\tau >T)+{\int }_T^{T+t}\lambda \tau f(\tau \mid \mu ,\tau >T)d\tau \\ & =\lambda t{e}^{-\mu t}+\lambda {\int }_0^t\mu \tau e^{-\mu \tau }d\tau \\ & =\frac{\lambda }{\mu }-\frac{\lambda }{\mu }{e}^{-\mu t}\end{array}$$

Of course we don’t know whether a customer is alive at $T$; therefore

$$E[Y(t)\mid \lambda ,\mu ,x,t_x,T]=E[Y(t)\mid \lambda ,\mu ,\text{ alive at }T]P(\tau >T\mid \lambda ,\mu ,x,t_x,T)$$

Also, since $\lambda$ and $\mu$ are unobserved, we need to integrate them out:

$$\begin{array}{c}E[Y(t)\mid r,\alpha ,s,\beta ,x,t_x,T]={\int }_0^{\mathrm{\infty }}{\int }_0^{\mathrm{\infty }}\{E[Y(t)\mid \lambda ,\mu ,\text{ alive at }T]P(\tau >T\mid \lambda ,\mu ,x,t_x,T)\\ g(\lambda ,\mu \mid r,\alpha ,s,\beta ,x,t_x,T)\}d\lambda d\mu \end{array}$$

After the tedious computation, we will get

Note that:

1. The first part, the bracketed term, is out expression for $P(\text{alive}|x,t_x,T)$.

2. The rest part is mean of the Pareto/NBD (2.1), with “updated” parameters that reflect the individual’s behavior up to time $T$ (assuming no “death” in $(0,T])$).

Next time, we’ll finally take about the prediction of CLV.