Survival Analysis in R
Here is some tutorial notes for “Survival Analysis in R” course.
-
Do patients taking the new drug survive longer than others?
-
How fast do people get a new job after getting unemployed?
-
What can I do to make my friends stay on the dancefloor at my party?
All these questions require the analysis of time-to-event data, also called survival analysis. Learn how to deal with time-to-event data and how to compute, visualize and interpret survivor curves as well as Weibull and Cox models.
R package 📦 we learned here is survival package.
Why Survival Analysis?
-
Time is always positive
-
Different measures are of interests
-
Censoring almost always an issue
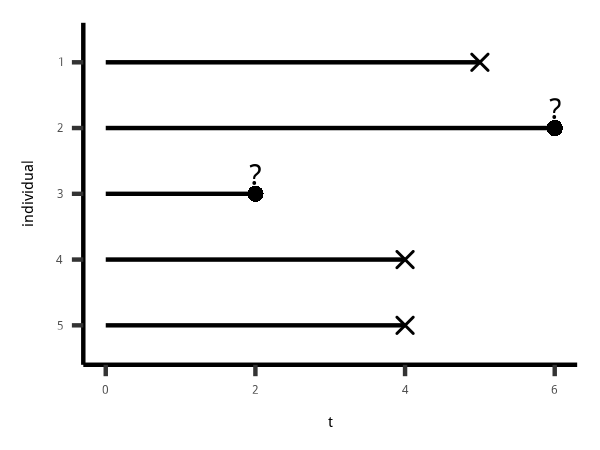
Survival Function
In probability class, we mainly focus on the PDF. While in the survival analysis, we are mainly focusing on the survival function.
$$S(t) = 1 - F(t) = P(T > t)$$
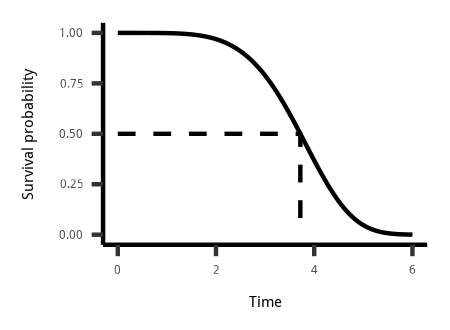
The above image shows an example of survival curve; the x-axis refers time and y-axis refers probability. One of the useful quantities is the median survival time.
You should know how to read and interpret the survival curve: $100\cdot\widehat{S(t)}$ percent of duration are longer than $t$.
Estimate Survival Curve
Kaplan-Meier estimate
Q: When does the Kaplan-Meier curve drop?
A: Drop when a event happens (eg. patient dies); stays the same when event censored (eg. patient censored) because we have no information on the censored people.
Weibull Model
The Weibull model is for estimating smooth survival curves.
Proportional Hazrds Model
Detailed Lecture Notes: The proportional hazards regression model.(From USCD Math 284)
Hazard Rate
When we are trying to model the effects of covariates (e.g. age, gender, race, machine manufacturer) we will typically be interested in understanding the effect of the covariate on the Hazard Rate. The hazard rate is the instantaneous probability of failure/death/state transition at a given time t, conditional on already having survived that long. We will denote it λ(t). Treating time as discrete:
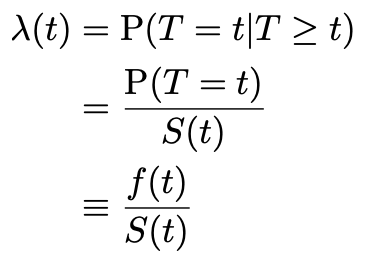
Key Points
Reference
-
The Cox Proportional Hazards Model. This blog provides a good, very easy to understand, introduction for survival analysis and the proportional hazards model.
