Introduction to Latent Dirichlet Allocation (LDA) Model

Motivation

Uncovering the insights from User-generated content (UGC) is important for researchers as UGC provides a rich information about consumer’s experiences with quality.

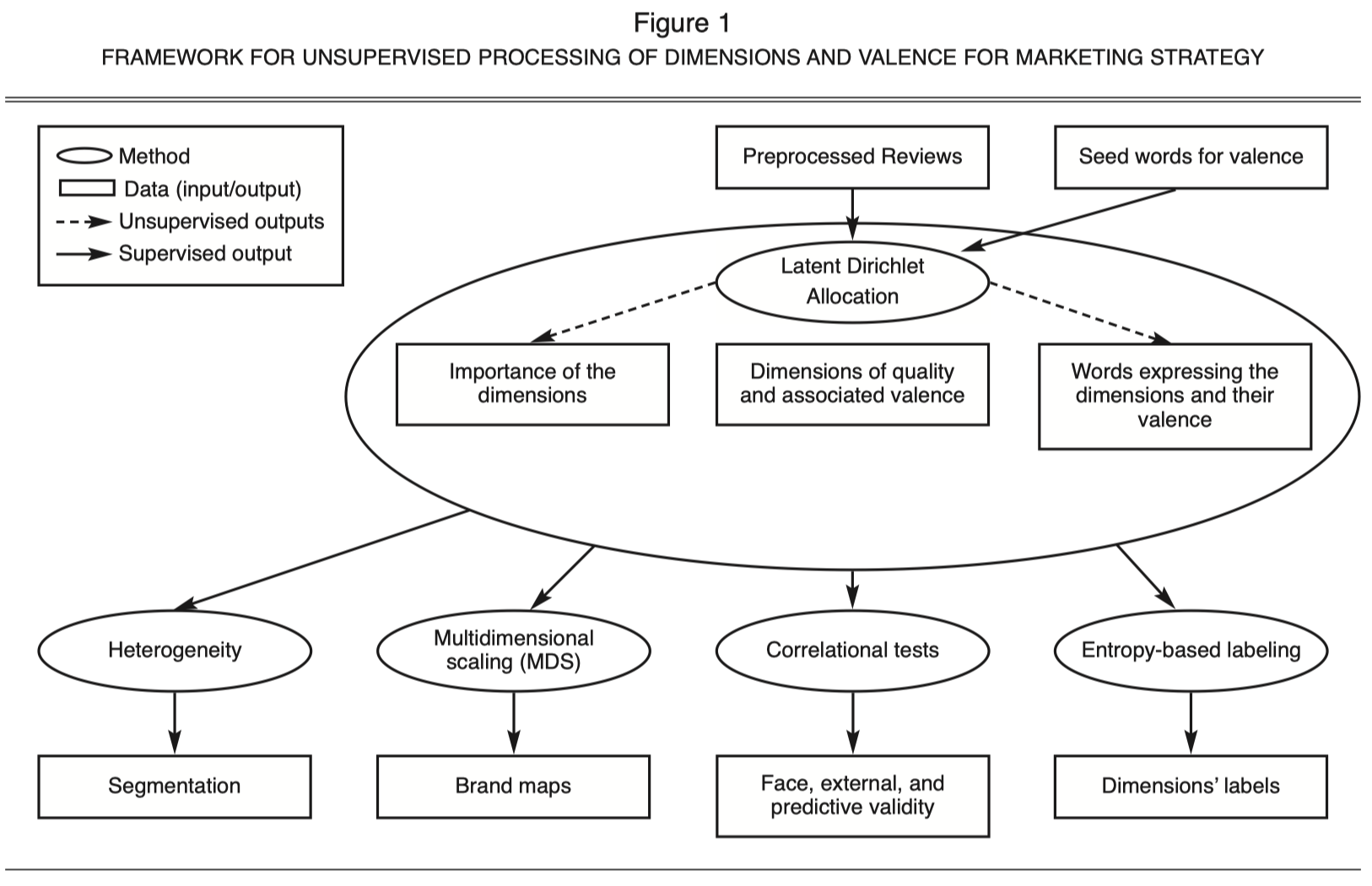
Tirunillai and Tellis (2014) propose a unified framework:

1. Extract the latent dimensions of quality from UGC

2. Ascertain the valence, labels, validity, importance, dynamics, and heterogeneity of those dimensions

3. Use those dimensions for strategy analysis (e.g., brand positioning)

LDA Model

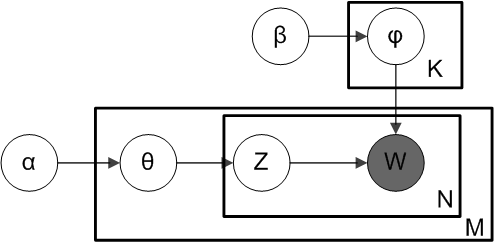
LDA is a generative probabilistic model used primarily for topic modeling in text. This model helps us discovering the hidden thematic structure in a large collection of documents.

Key Idea

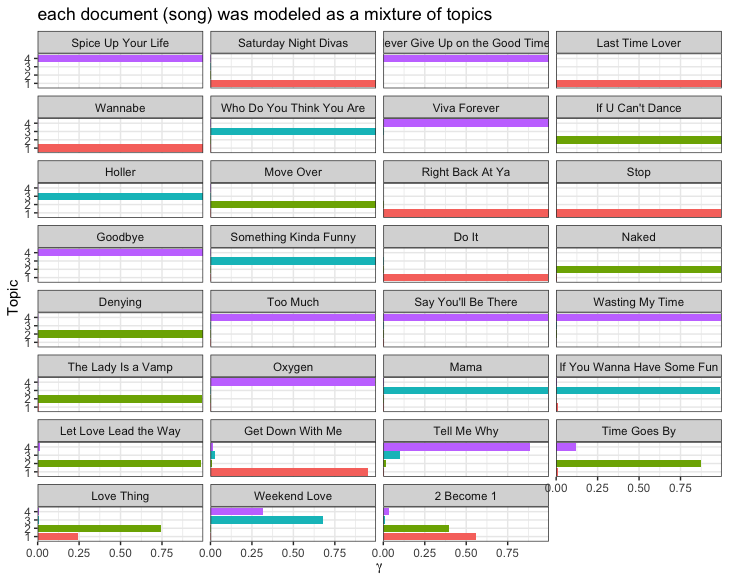
• Every document is a mixture of topics.

• Every topic is a mixture of words.

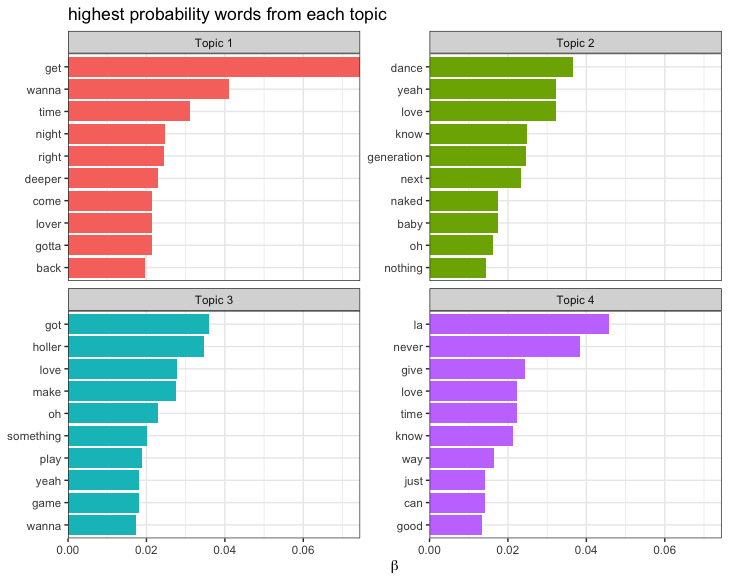
LDA is a mathematical method for estimating both of these at the same time: finding the mixture of words that is associated with each topic, while also determining the mixture of topics that describes each document.

LDA R Code Example

Many awesome R packages to implement LDA. For example, this blog post tutorial by Julia Silge walks through how to build a structural topic model and then how to understand and interpret it.

library(stm)
topic_model <- stm(lyrics_data, K = 4)
Copy

• The most important parameter when training a topic modeling is k, the number of topics.

• This is like k in k-means in that it is a hyperparamter of the model and we must choose this value ahead of time.

• We can find the best value for k using data-driven methods.

Dirichlet and Categorical distributions

As we are familiar with Beta and Bernoulli distributions, it is not hard to understand the Dirichlet and Categorical distributions, which are natural extensions of previous ones.

Mathematical Components of LDA

0. Model Setup:

• Topics: $K$ topics.
• Documents: $D$ documents.
• Words: $V$ words in the vocabulary.

1. Topic Distribution for Each Document:

• Each document $d$ has a topic distribution ${\theta }_d$.
• ${\theta }_d\sim \text{Dirichlet}(\alpha )$.
• Here, $\alpha$ is a $K$-dimensional vector, where $K$ is the number of topics.

2. Word Distribution for Each Topic:

• Each topic $k$ has a word distribution ${\varphi }_k$.
• ${\varphi }_k\sim \text{Dirichlet}(\beta )$.
• $\beta$ is a $V$-dimensional vector, where $V$ is the vocabulary size.

3. Generative Process for Each Document:

• For each document $d$:

  • Draw topic distribution ${\theta }_d\sim \text{Dirichlet}(\alpha )$.

• For each word $n$ in document $d$:

  • Draw topic $z_{d,n}\sim \text{Multinomial}({\theta }_d)$.
  • Draw word $w_{d,n}\sim \text{Multinomial}({\varphi }_{z_{d,n}})$.

4. Inference Problem:

• Compute posterior distribution:

  $P(\theta ,z|w,\alpha ,\beta )=\frac{P(\theta ,z,\varphi ,w|\alpha ,\beta )}{P(w|\alpha ,\beta )}=\frac{P(w|z,\varphi ),P(z|\theta ),P(\theta |\alpha ),P(\varphi |\beta )}{P(w|\alpha ,\beta )}$

• Exact computation is intractable. Gibbs sampling or variational inference are used.

5. Hyperparameters $\alpha$ and $\beta$:

• $\alpha$ and $\beta$ are hyperparameters of the Dirichlet distributions.

• $\alpha$: Affects the mixture of topics in each document.

• $\beta$: Affects the distribution of words in each topic.

6. Why Dirichlet Distribution?

• In LDA, topics and words are assumed to be multinomially distributed.

• Dirichlet is the conjugate prior to the multinomial, which simplifies computation, especially for Bayesian inference.

• $X\sim Dirichlet(\alpha )$ with pdf $$f(X;\alpha )=\frac{1}{B(\alpha )}\prod _{i=1}^K{x}_i^{{\alpha }_i-1}$$

• Dirichlet distribution is a generalization of the Beta distribution.

  • Binomial Likelihood 🤝 Beta Prior
  • Multinomial Likelihood 🤝 Dirichlet Prior

Reference

• Tirunillai, S., & Tellis, G. J. (2014). Mining Marketing Meaning from Online Chatter: Strategic Brand Analysis of Big Data Using Latent Dirichlet Allocation. Journal of Marketing Research, 51(4), 463–479. https://doi.org/10.1509/jmr.12.0106

• Julia Silge’s tutorial Topic modeling for #TidyTuesday Taylor Swift lyrics