A Story Behind Maximum Likelihood
TL;DR
What are we actually doing on MLE? What is the motivation for the Maximum Likelihood Estimation? In this post, we will go over the story behind the maximum likelihood.
We’ll first talk about the total variation distance, which is a very intuitive measure to tell you how “close” our estimator is from the true parameter.
Next, let’s move to KL-divergence used to replace the total variation distance.
In the end, we’ll minimize the KL-divergence to get the “good” estimator. In this process, the maximum likelihood principle will come in.
Total Variation Distance
How to define a “good” estimator?
A “good” estimator should be very “close” to the true parameter isn’t it?
Click to view the formal setting
Definiton of Totol Variation Distance
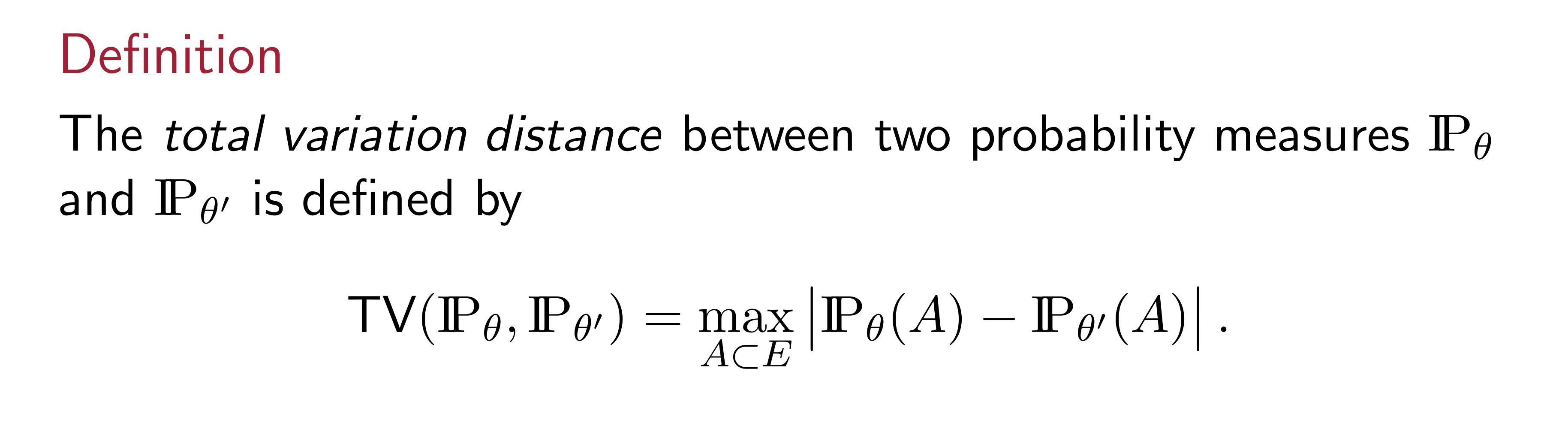
This definition is very intuitive but pretty strong and hard to calculate right? Because you have to find the maximum over all possible sets. The good news is, we also have this formulation:
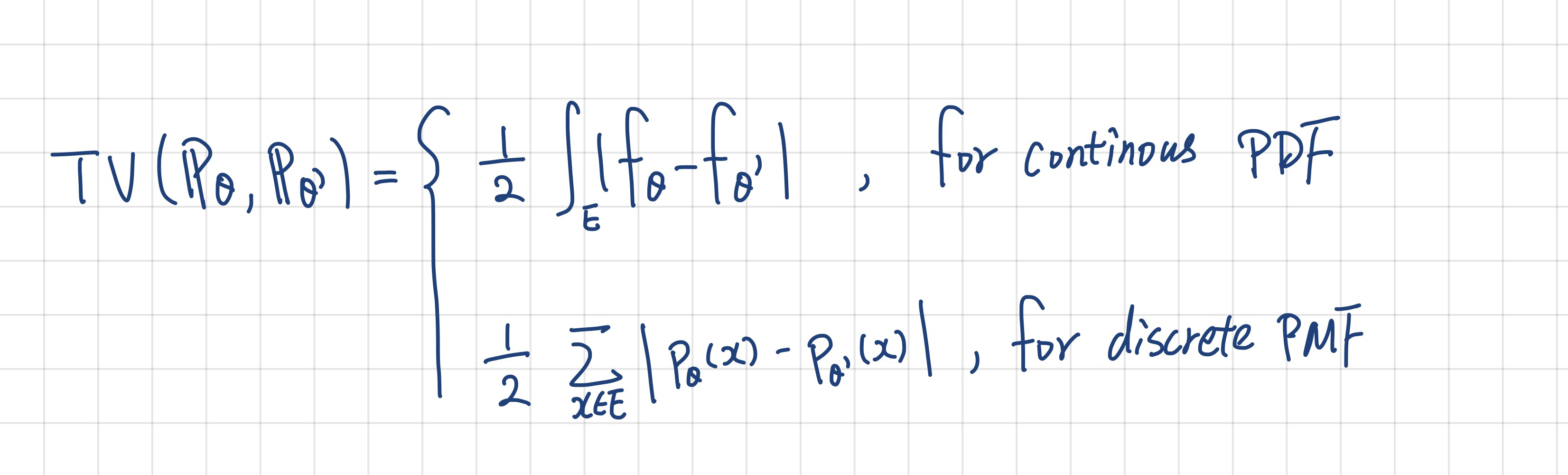
Click to view the formal statement.
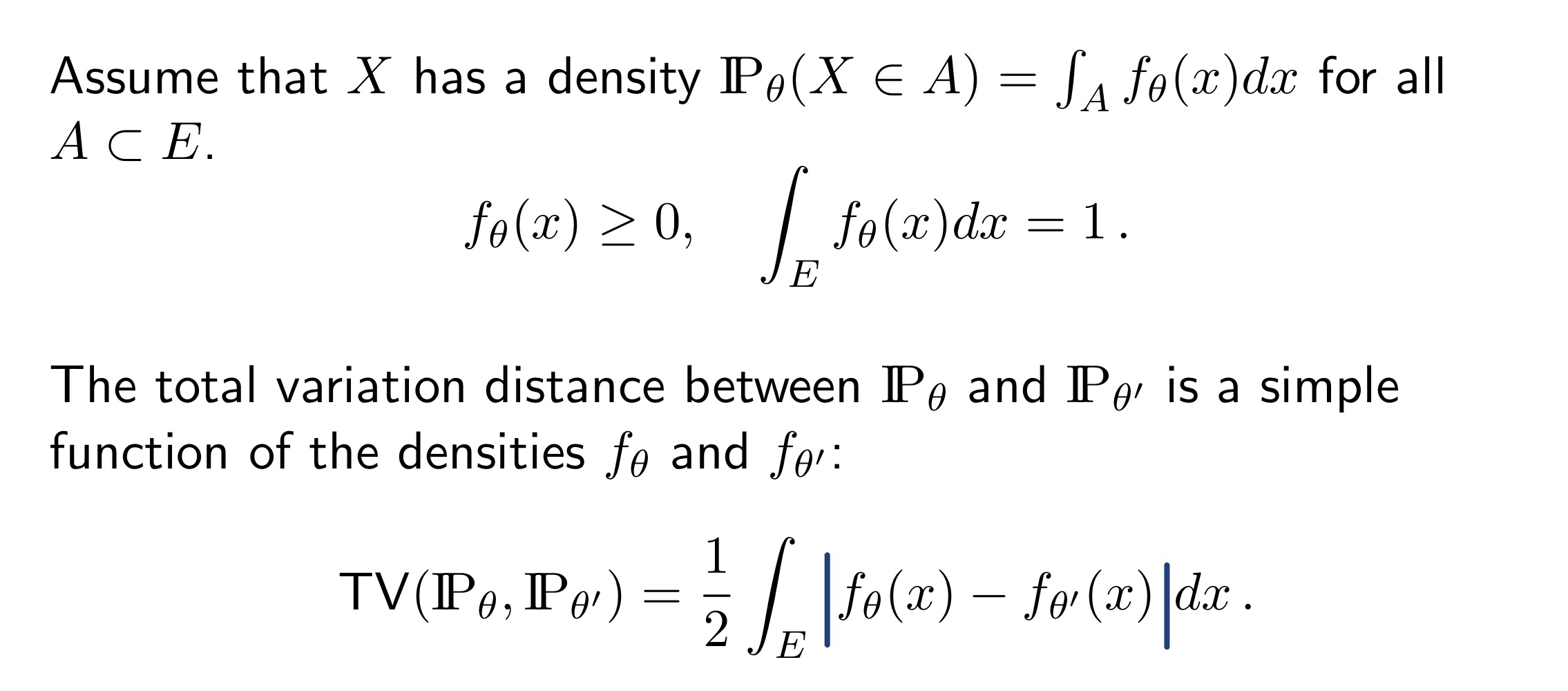
Before the proof, let’s use the graph to get some feeling for the equation. Where does the 1/2 come from?
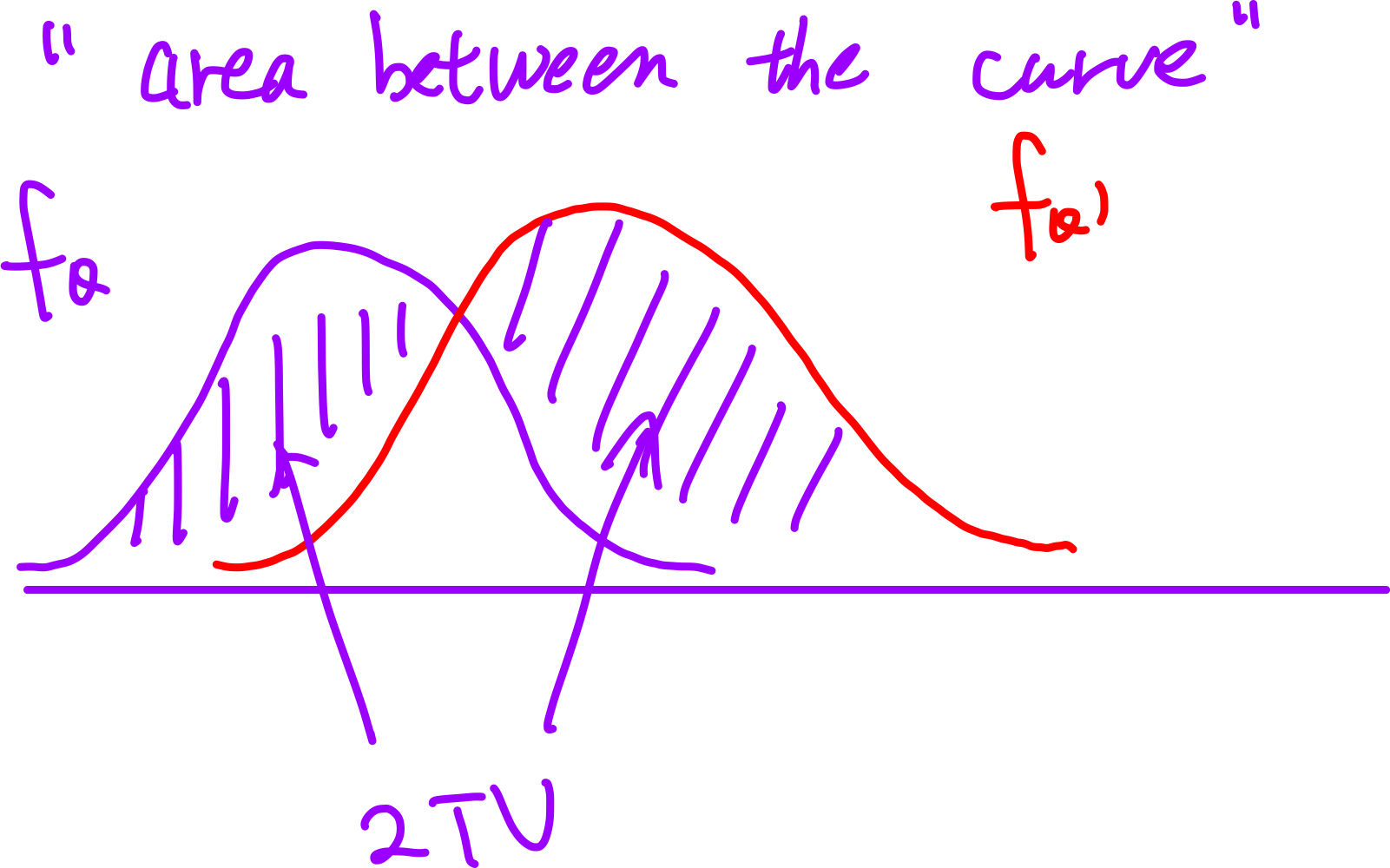
Proof:
Click to view the proof
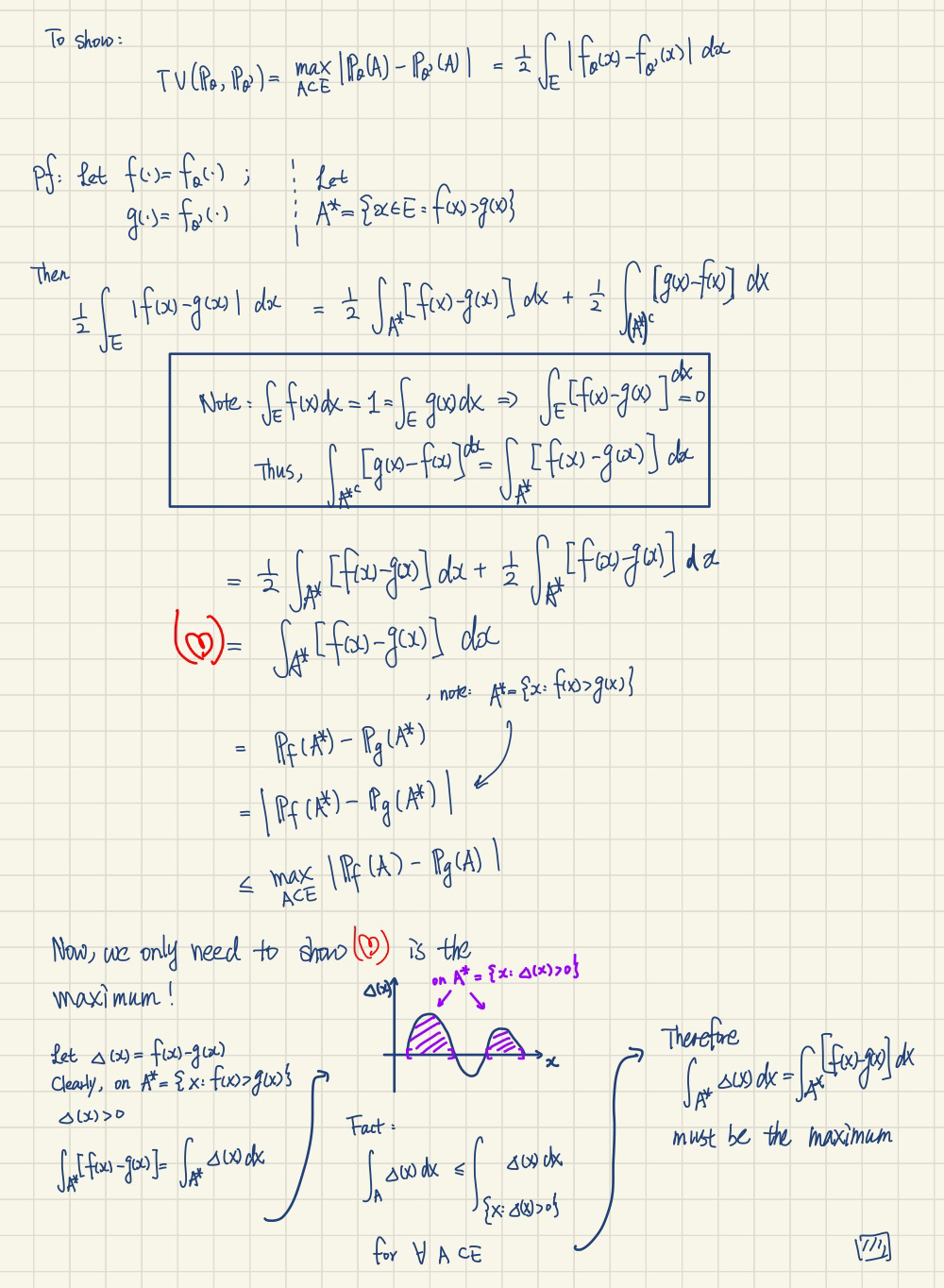
Note that, the key part in the proof is the observation: $$\int f = \int g = 1 \implies \int f - g = 0,$$ Then we have $$\int_{\{x: f-g > 0\}} f - g = \int_{\{x: f-g < 0\}} g - f.$$
Properties of TV
Total variation is symmetric, non-negative, definite and satisfies the triangle inequality.
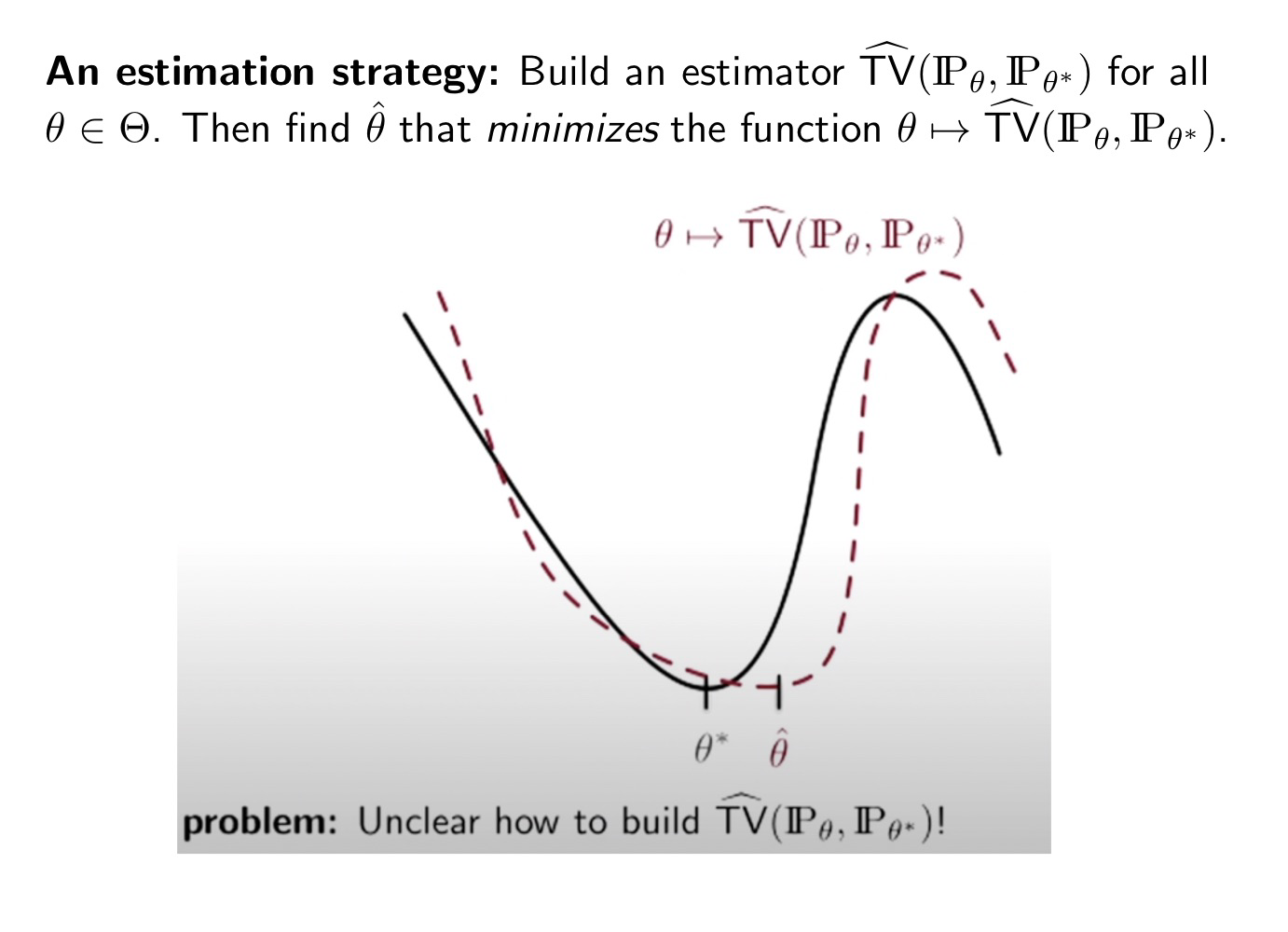
Unclear how to estimate TV!
Our goal is to find the “good” estimator.
If using Total Variation distance to describe the “close”, we need to :
-
Build an estimator $\widehat{TV}(\mathbb{P}_{\theta}, \mathbb{P}_{\theta^*})$.
-
Find $\hat{\theta}$ that minimize the function.
However, it is unclear how to build $\widehat{TV}(\mathbb{P}_{\theta}, \mathbb{P}_{\theta^*})$!
-
We don’t know the $f_{\theta^*}$ (the true parameter $\theta^*$ is unknown), and it is very hard to manipulate the integral of density difference.
-
The common strategy is to replace the expectation ($E(\cdot)$ ) with the average ($\frac{1}{n}\sum_n(\cdot)$ ), but there is no clear expectation in $TV(\cdot)$.
Due to above difficulties, we need a more convenient distance between probability measure to replace total variation. This is the motivation for DL divergence.
REMARK:
The total variation distance, describing the “worst” scenario, is very intuitive and has a clear interpretation. However, it is hard to build an estimator. That’s why we move to KL divergence.
KL divergence
Let’s check the definition first,
For the second property (non-negative), we can use Jensen’s inequality to show it.
KL 🤝 MLE
Now we are ready to introduce maximum likelihood principle using the KL-divergence.
Summary
What are we actually doing on MLE?
The short answer is we are minimizing the KL-divergence.
Reference
